一路上感謝各位讀者們的支持和回饋。
本 30 天系列文目前已經將篇幅重新整理、編纂成冊。
《JavaScript 概念三明治》在天瓏書局上架囉!
喜歡這個系列,想閱讀更詳細原理說明的讀者可以參考:
https://www.tenlong.com.tw/products/9789864347575
隨著硬體規格條件的提升, 網站商業邏輯的運作也慢慢從以往的後端伺服器轉移到客戶端,因此前端領域的專業知識就變得越來越重要,隨著前端技術被重視,也開始慢慢出現 React 、 Vue 、 之類前端框架的生態圈出現,而後端則慢慢演變為單純的 API 伺服器負責提供資料的存取端口。同樣的,畫面的互動也是另一個越來越被注重的部分,因此怎麼實作出更精緻優雅的前端介面以及互動邏輯也是前端工程師們面臨的新挑戰之一。這些在在的都考驗了工程師們對 JS 這個語言本身更全面的了解。
如同前面所說,隨著商業邏輯慢慢著重在前端,許多資料的規格訂定也常常會跟隨著介面的結構而有所不同,這些隨著前端邏輯而被暫存在前端的資料,變得有點像是後端伺服器放在前端的副本。所以,前端工程師的經驗跟專業,就會在資料結構的選擇與判別使用的時機的能力上顯現出差異,而某些資料結構我們在前面的文章多多少少都有提到一些了。在這篇文章內,我想較全面的,對在開發上,常使用到或常見的資料結構做一些說明。
基本上有三種類型資料結構:
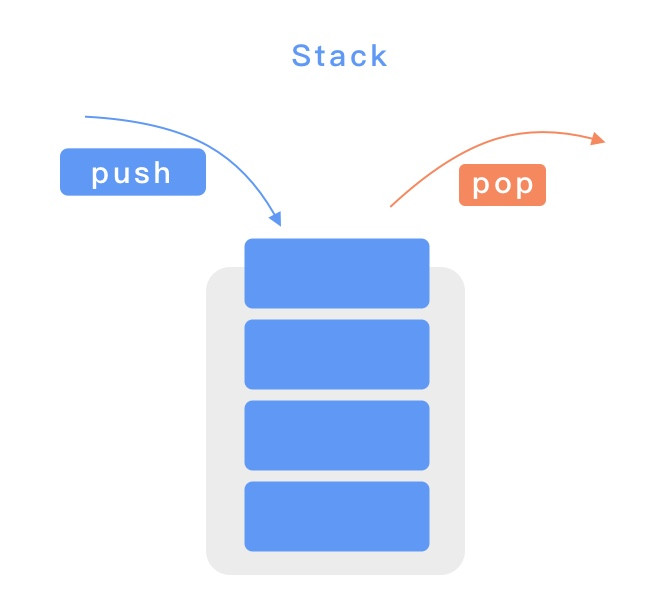
Stack 具有後進後出的特性,堆疊的概念我相信各位 JS 工程師都已經非常熟悉了,而這大概也是 JS 內最重要的資料結構了,在之前講到執行環境堆疊的時候有提過。以程式的方式來說,堆疊的結構就是一個具有 push 跟 pop 兩個方法的陣列,push 可以把元素放到堆疊的最上層,而 pop 可以把元素從堆疊的最上層拿出來。
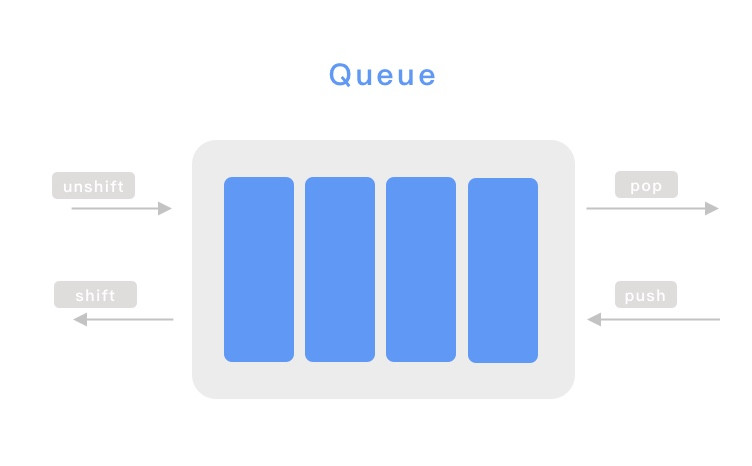
Queue,序列 也是 JS 語言的核心部分之一,Queue 具有「先進先出」的特性,還記得我們之前提到的 Event Queue 、 MacroTask Queue 以及 MicroTask Queue 嗎?因為有了 Queue 這種樣子的資料結構,JS 才能夠具有非同步這麼具有識別度的特性。那麼以程式的角度來看,Queue ㄧ樣是有兩種方法的陣列:unshift 與 pop。 unshift 可以把元素放到 Queue 的最尾端,而 pop 則是把元素從最前端取出來,Queue 也可以反向操作,只要把 unshift 與 pop 換成 shift 與 push。
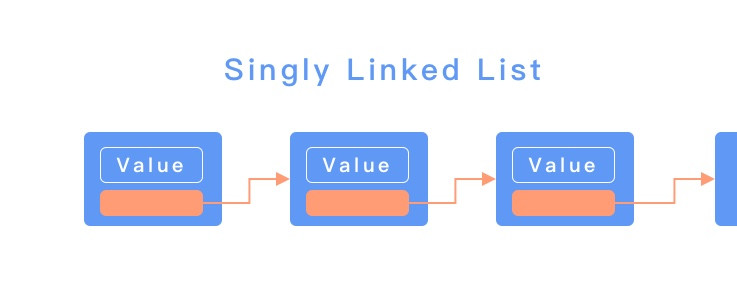
Linked List ,鏈結串列是一種有序的、且線性的資料結構,在 Linked List 上每一筆資料都可以被看作是一個節點 ( Node ),每個節點上都包含了兩個資訊:一個是要儲存的數值、一個是指向其他節點位置的指標。Linked List 具有以下特性:
head ,是一個指向第一個節點的參考指標tail 節點,是指向最後一個節點的參考指標null
Linked List 基本上有 單向( singly ) 跟 雙向 ( doubly ) 兩種類型,在單向的鏈結串列中,只存在一個指向下一個節點的指標。
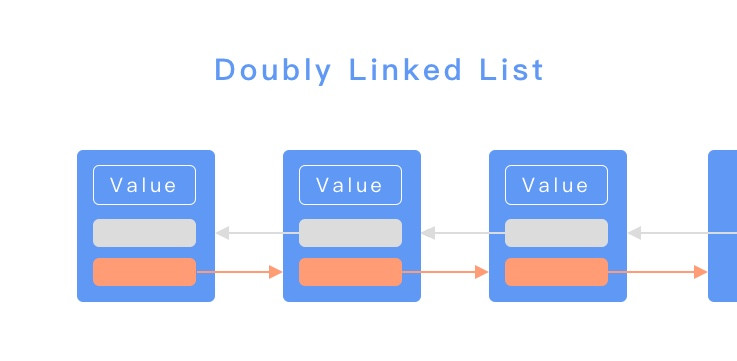
而在雙向的鏈結串列中,則會有兩個指標,一個指向上一個節點,一個指向下一個節點。
Linked List 由於結構的關係,可以在頭、尾,任何地方插入節點,因為只要改變指標的指向就可以了,所以只要搞懂運作方式,他也能實現前面提到的 Queue 跟 Stack 結構的行爲。Linked List 在前後端開發上也很有幫助,在前端 React 框架常常搭配使用的狀態管理器 Redux 中,從畫面到 Action 到 Reducer 這樣子的資料流,就使用了 Linked List 的思考方式,來決定資料的下一個目標( 函式 )。在後端 Express 框架上則用 Linked List 來處理 Http Request 與 Middleware 層的資料流動。
接下來讓我們以雙向的鍊結串列來看看實際上在 JS 內是怎麼使用的,首先我們會需要節點的類別,這樣我們就可以自己指定節點跟下一個節點:
class LinkedNode {
constructor(value,prev,next){
this.value = value;
this.next = next;
this.prev = prev;
}
}
let head = new LinkedNode(null,null,null)
let node1 = new LinkedNode(1,head,null)
let node2 = new LinkedNode(2,node1,null)
let node3 = new LinkedNode(3,node2,null)
node1.next = node2
node2.next = node3
然後我們可以再創一個 LinkedList 類別來記錄這些節點間的關係,
class LinkList {
constructor(value,prev,next){
this.head = null
this.tail = null
this.lenght = 1
}
addToHead(){
}
}
Linked List 要能再頭地方加入新的節點成為新的 head,因此加入輔助函式看看:
class LinkedNode {
constructor(value,prev,next){
this.value = value;
this.next = next;
this.prev = prev;
}
}
class LinkList {
constructor(value){
this.head = null
this.tail = null
this.addToHead(value)
this.lenght = 0
}
addToHead(value){
const newNode = new LinkedNode(value);
newNode.next = this.head; // 讓原本的 head 成為新節點的 next
newNode.prev = null // head 並沒有前一個節點
this.head = newNode // 最後把原來的 head 換成新的節點
this.lenght += 1
return this.head
}
}
let newList = new LinkList('first')
newList.addToHead('second')
newList.addToHead('third')
newList.head.value // third
newList.head.next.value //second
newList.head.next.next.value //first
接下來我們再實作一個可以從中間刪除任意節點的方法,要找到 Linked List 的某一個數值並且刪除,就只能用尋訪的方式一個一個尋找,這裡我們用 while 回圈以一個類似遞迴的方式來尋找:
class LinkList {
constructor(value){
this.head = null
this.tail = null
this.addToHead(value)
this.lenght = 0
}
addToHead(value){ ... }
removeFromHead(){
if(!this.head.next) this.head.next = null
const value = this.head.value;
this.head = this.head.next
this.length--
return value
}
remove(val) {
if(this.length === 0) {
return undefined;
}
if (this.head.value === val) {
this.removeFromHead();
return this;
}
let previousNode = this.head;
let thisNode = previousNode.next;
while(thisNode) {
// thisNode 的參考會隨著 while 而不斷的往 next 去尋找
if(thisNode.value === val) {
break;
}
previousNode = thisNode; // 同時也會不斷紀錄前一個節點
thisNode = thisNode.next;
}
if (thisNode === null) {
return undefined;
}
previousNode.next = thisNode.next; // 一旦成功找到要刪除的節點,才能夠順利銜接前後節點,達到刪除的效果
this.length--;
return this;
}
}
示範實做跟說明幾個函式到這邊,基本上只要知道怎麼修改節點的指向,就可以了解怎麼實作這些操作 Linked List 的方法,包括從 head 刪除節點、從中間新增、刪除節點,以及從最後面新增、刪除,讀者可以自己練習完成看看。
樹的結構跟 Linked List 有點像,也是從一個節點開始往下長,差別在於 Linked List 裡一個節點只能對到另一個節點,而在樹狀結構內,一個節點可以對到好幾個其他節點,也稱為子節點( Child Node ) ,之前我們講到的 DOM ,正是一種樹狀結構,最上層的 html 是上層節點,而往下延伸出 body 與 head 等下層子節點。
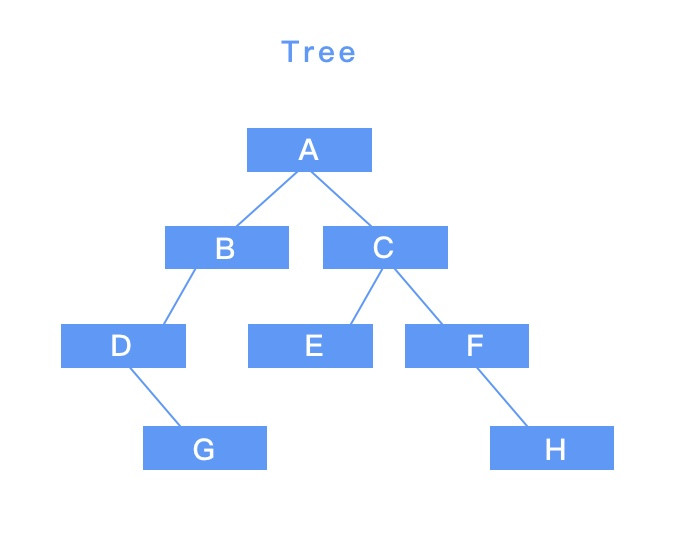
而樹的結構也可以被加上特殊的規則,例如常聽見的二元樹結構, 就是從樹狀結構演變而來,因為在二元樹裡面,每個節點被規定只能擁有另外兩個子節點。而且左邊子節點的數值只能小或等於父節點的數值,而右邊子節點的數值必須大於父節點的數值,以這樣子排列方式,我們就可以有規律的去搜尋或是操作我們需要的節點,例如,整個二元樹的最小值可以在最左邊且最後代的子節點被找到,反之在最右邊後代節點則可以找到最大值。
在樹的搜尋上則有兩種相似的方式:
深先搜尋 ( Depth-First Traversal, DFT ) :
把樹想成由最上面開始往下生長的結構,深先搜尋就是從最上面的根節點,往下垂直的搜尋,深先搜尋裡又分為三種走訪順序,以上面的二元樹圖為例,分別是:
前序 ( Pre Oreder ) :
順序:訪問根節點 → 訪問左子樹 → 訪問右子樹
上圖順序: A → B → D → G → C → E → F → H
中序 ( In Order ) :
順序:訪問左子樹 → 訪問根節點 →訪問右子樹
上圖順序: D → G → B → A → E → C → F → H
後序 ( Post Order ):
順序:訪問左子樹 → 訪問右子樹 → 訪問根節點
上圖順序: G → D → B → E → H → F → C → A
廣先搜尋 Breadth-First Traversal , BFT )
廣先搜尋則跟深先搜尋相反,是以水平方向為主的搜尋方式,在樹狀結構裡面,每往下長出一個子節點,就會被視為一層。深先搜尋在執行時是先查看節點有無子節點,如果有的話就盡量往下去搜尋,而廣先搜尋則是在搜尋時先檢查子節點有無其他同一層的節點,然後將這些同層子節點記錄下來,一個一個去搜尋,因此在執行廣先搜尋時,必須用到 Queue 來輔助。
上圖順序: A → B → C → D → E → F → G → H
樹狀結構與前面鍊狀串列結構實作方法相似,而且樹狀結構若要往下探討可以有很多種變形,例如把不同層的節點串在一下之後就會變成複雜的圖 ( Graph ),這些內容多到可以再寫一篇文章,因此在這邊先不提供範例。
雜湊表是根據鍵值 ( Key ) 來查找對應記憶體位置的資料結構。陣列就是一個很類似 Hash Table 的結構,只不過陣列是利用「索引」來查找資料,因此只能是數字。
可以把 Hash Table 想成是建立在陣列上,透過將不同字串轉成對應的陣列索引來查找,而達到比較靈活的鍵值查找,要達到這樣子的效果,我們會需要實作一個 Hash Function ,來把字串轉換成索引。
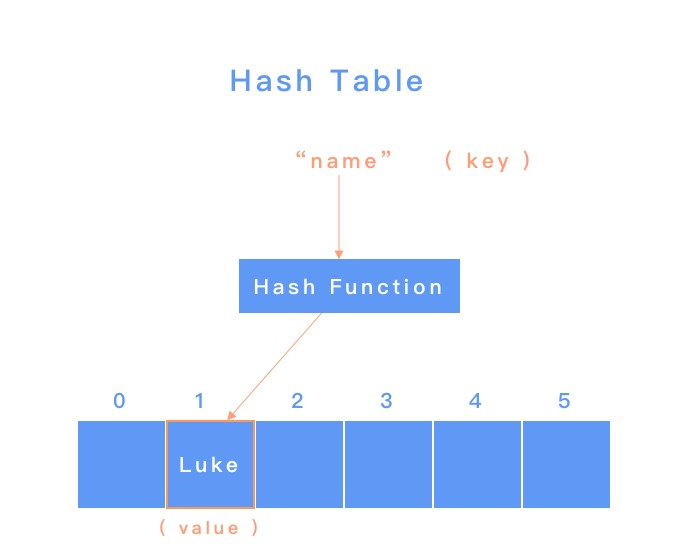
Hash Function 的運作方式大概會是給每個字元對應的可運算數值,當要查找的時候就把字串內所有字元的數值加起來然後給陣列當成索引值,如果加起來的數值太大,陣列沒有那麼多空間,就必需透過另外的規則簡化(如:加完的數值 mod 10 ) 來取得對應、可行的索引。
getCharNum(char){
return charCodeAt(char)
}
hashFunction (key) {
let hashCode = 0
key.split('').forEach(char=>{
hashCode += getCharNum(char)
})
return hashCode % 10
}
上面是一個 hash function 的實作,當然這只是簡化的範例而已,真正應用在現代系統環境的實作邏輯複雜非常多。透過 Hash Table 的運作方式我們可以利用字串來存取對應的數值,有沒有覺得很熟悉,想到什麼?沒錯就是 JS 的物件!從結果來看 JS 的物件非常像是 Hash Table 的結構,不過根據我的調查結果,有一說是這點會根據 JS 引擎的實作而有所差異,有些引擎裡面是透過混合 Linked List 跟 Hash Table 兩種資料結構來實作物件。
終於講完了這些常見的資料結構,看完之後你應該可以發現這些資料結構大概有一半在前面 JS 相關內容都有提到,分別是:
這些部分如果不深入去看這個語言運作方式的話是不會發覺的,這些資料結構也可以應用在許多系統資料的運算。雖然這個章節只能很粗淺的介紹,但我希望讓原本不熟悉資料結構的人,下次再看到類似的東西可以不會那麼害怕,也能夠更冷靜地往下研究原本要鑽研的知識細節。
Objects and Hash Tables in Javascript
